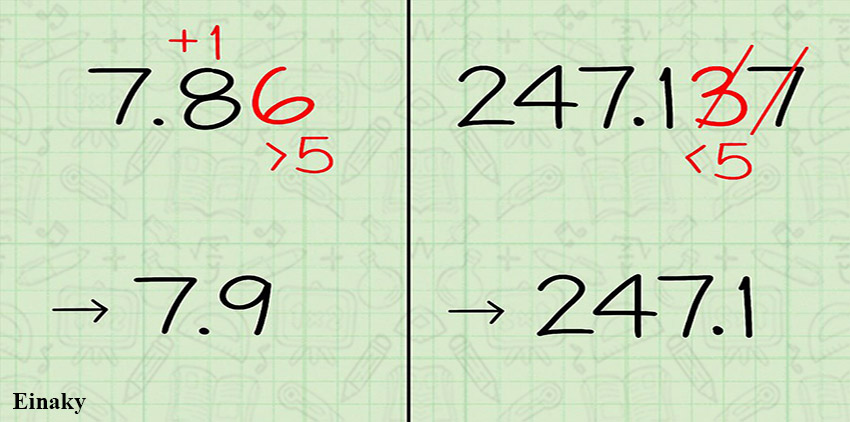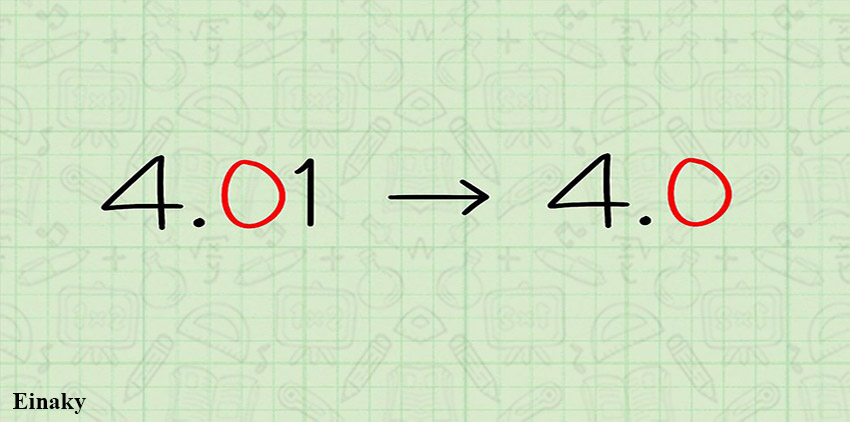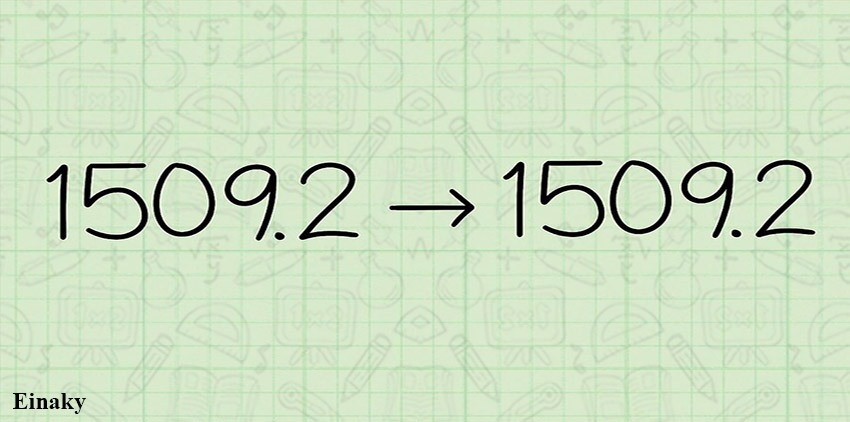چطور یک عدد را گرد کنیم؟

• توضیحات

آیا برای شما هم پیش آمده که در بین اعداد زیادی گیر افتاده باشید و ندانید چه راهی برای ساده کردن آنها وجود دارد؟

در این مواقع گرد کردن اعداد به کمک شما می آیند.

با گرد کردن اعداد ، انجام عملیات روی آنها ساده تر می شود.

اگر نمیدانید که چگونه اعداد را گرد کنید ، در این مقاله به صورت قدم به قدم شما را با روند گرد کردن اعداد آشنا میکنیم.

در انتهای این مقاله شما میتوانید هر عدد چه منفی ، چه طولانی و … را گرد کنید.

بخش اول: آموزش گرد کردن اعداد

1- راهنمای کلی گرد کردن اعداد با استفاده از محور اعداد (مطالعه اختیاری)

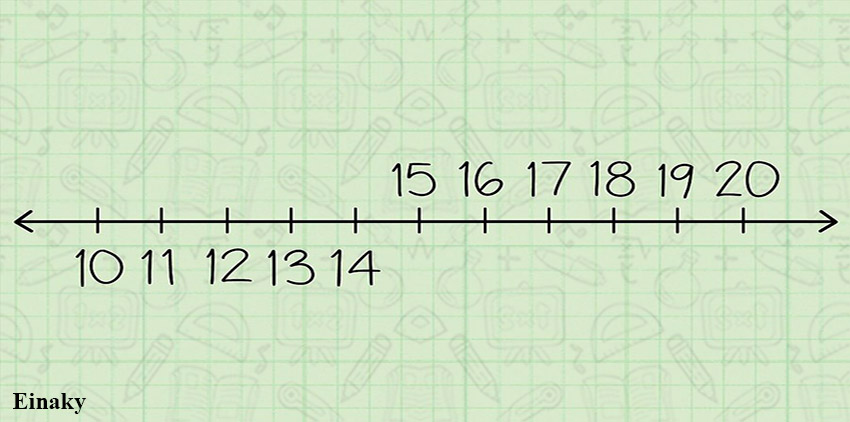
یک روش کوتاه برای گرد کردن اعداد این است که میتوانید بخش اعشاری عدد را برای لحظه ای نادیده بگیرید، سپس روی یک کاغذ، یک محور اعداد از شماره 10 تا 20 بکشید.

اعداد کمتر از 15 مثل 13 یا 11 به 10 نزدیک تر هستند و پس میتوانید آنها را به 10 گرد کنید.

اعداد بزرگتر از 15 مثل 18 یا 16 به 20 نزدیک تر هستند و درنتیجه میتوانید آنها را به 20 گرد کنید.

برای بخش اعشار هم میتوانید همین روند را در پیش بگیرید به این صورت که یک محور اعداد از 0.10 تا 0.20 بسازید و سپس آنها راگرد کنید.

2- مهم نیست عدد شما چند رقم اعشار دارد!

یک عدد روی کاغذ بنویسید، مهم نیست چند رقم اعشار داشته باشد.

میخواهیم در این مقاله به شما این را ثابت کنیم که عددهای طولانی با اعشار بالا ترسناک نیستند!
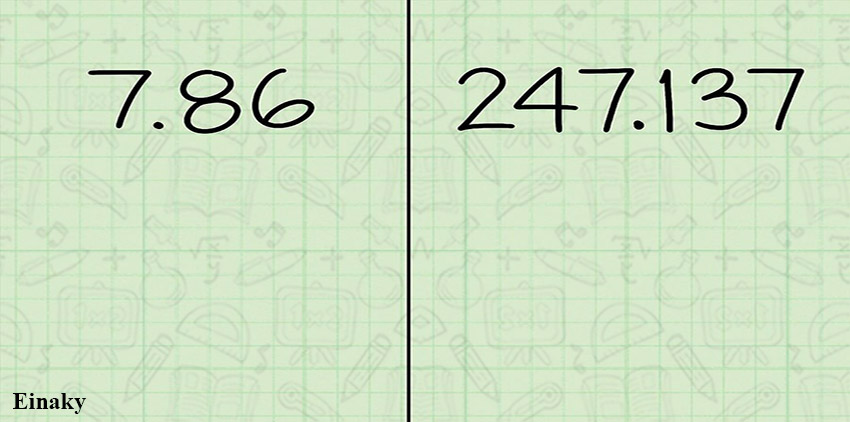
برای مثال ما در اینجا دو عدد 7.86 و 247.137 استفاده می کنیم. شما میتوانید هر عدد دیگری را مثال بزنید.

3- عدد دهم اعشار را پیدا کنید.

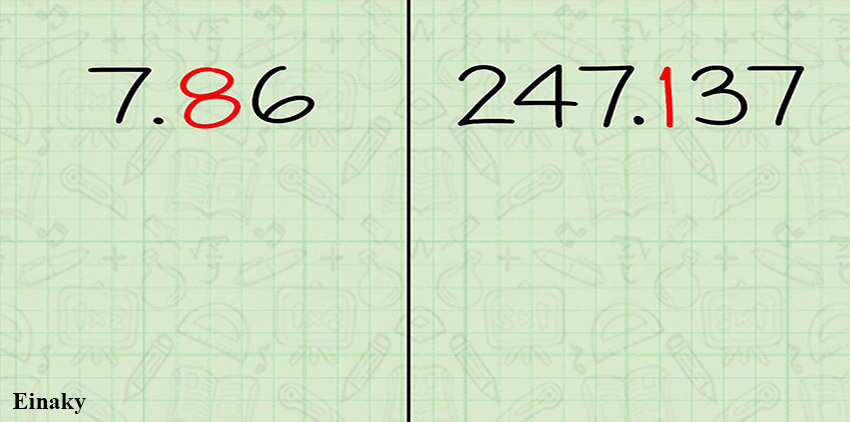
عدد دهم عدد اعشاری دقیقاً اولین عدد بعد از ممیز است. آن را پیدا کنید و زیر آن یک خط بکشید.
برای مثال عدد دهم 7.86 عدد 8 است.
و عدد دهم 247.137 عدد 1 است .

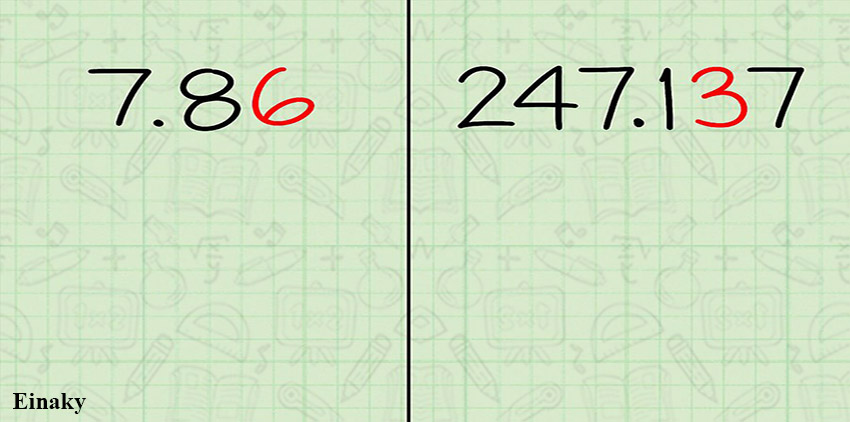
4- عدد صدم اعشار را پیدا کنید.

عدد صدم نیز عدد دوم بعد از ممیز است. این رقم به شما میگوید که عدد باید به سمت بالا گرد شود یا پایین.

این عدد را نیز پیدا کنید و زیر آن یک خط بکشید.
برای مثال عدد صدم 7.86 عدد 6 است .
و عدد صدم 247.137 عدد 3 است .
اعداد بعد از عدد صدم اهمیت چندانی ندارند و به آنها اصطلاحاً رقم های اضافی میگویند و تاثیر خیلی کمی در ارزش عدد دارند و میتوان آنها را نادیده گرفت.

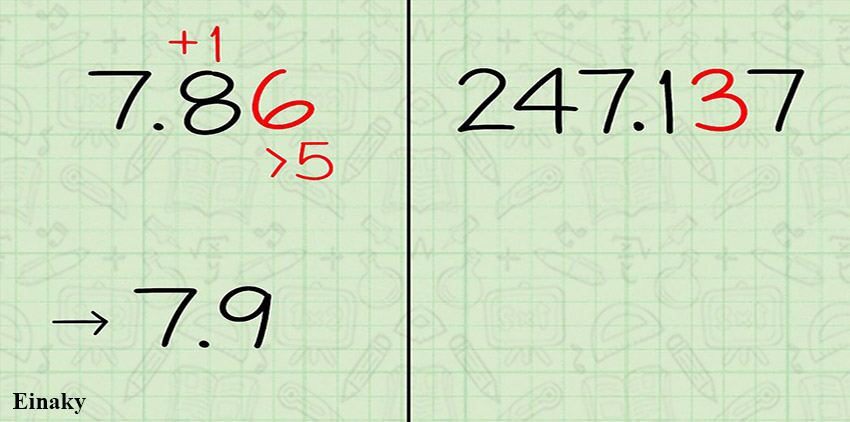
5- اگر عدد صدم از 5 بیشتر است، عدد دهم را به بالا گرد کنید.

اگر عدد صدم از 5 بیشتر است به عنوان مثال 8 است، به عدد دهم یک عدد اضافه کنید و سپس تمام اعداد بعد از عدد دهم را خط بزنید.

گرد شده عدد به دست آمد !

برای مثال عدد صدم 7.86 ، 6 میباشد و  از 5 بیشتر است.

پس باید یکی به عدد دهم یعنی 8 اضافه کنیم و بقیه اعداد بعد از عدد دهم را خط بزنیم. یعنی در نهایت عدد ما به شکل 7.9 در می آید.

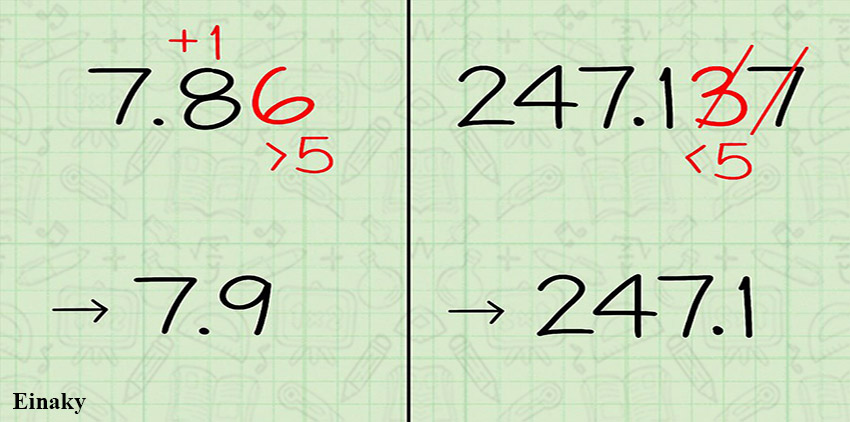
6- اگر عدد صدم از 5 کمتر است، عدد دهم را به پایین گرد کنید.

اگر عدد صدم به عنوان مثال 4 یا کمتر از 4 مثلاً 0 است، فقط کافی است که اعداد بعد از عدد دهم را خط بزنید. در نهایت شما عدد گرد شده را دارید.

برای مثال عدد صدم 247.137 از 5 کمتر است، پس باید تمام اعداد بعد از عدد دهم را نادیده بگیریم و در نهایت عدد گرد شده ما به شکل 247.1  به دست می آید.

بخش دوم: موارد استثنا در گرد کردن اعداد

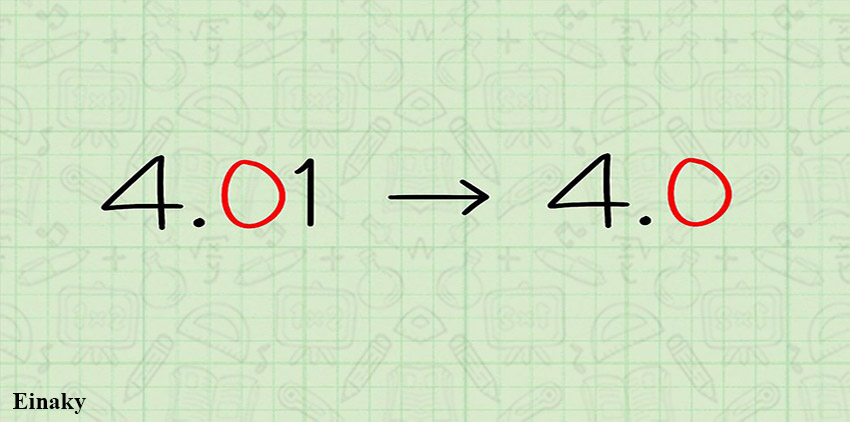
1- عدد صفر را نادیده نگیرید.

اگر عدد دهم صفر است، بعد از گرد کردن باید آن را بنویسید.

برای مثال عدد 4.03 چون عدد صدم آن از 5 کمتر است، فقط کافیست که عدد های بعد از عدد دهم را خط بزنید و عدد گرد شده 4.0 میباشد.

درست است که 4 با 4.0 تفاوتی ندارد و اشتباه هم نیست اما 0 دقت آن را بالا میبرد.

2- گرد کردن اعداد منفی

گرد کردن اعداد منفی نیز مشابه گردن کردن اعداد مثبت است و برای آنها نیز باید از مراحل مشابهی استفاده کنید با این تفاوت که علامت منفی را پیوسته بنویسید.

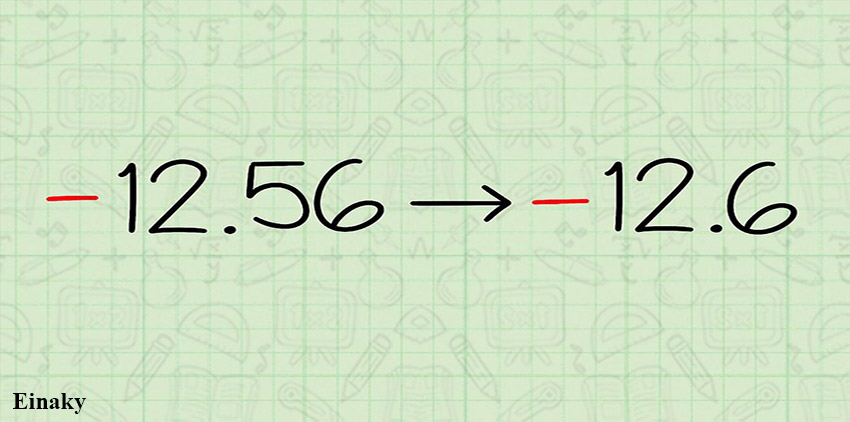
برای مثال گرد شده عدد -12.56 عدد -12.6 است و گرد شده عدد -400.333 نیز عدد -400.3 است.
در مورد اعداد منفی نیز بهتر است حواستان به عبارت های “گرد کردن به سمت پایین” یا “گرد کردن به سمت بالا” باشد.

برای مثال وقتی عدد -12.56 را به -12.6 گرد میکنید اگر عدد منفی نباشد در اصل به بالا گرد شده اما وقتی منفی است به خانه پایین تری از محور اعداد انتقال میابد و این یعنی عدد به سمت پایین گرد شده.

3- گرد کردن اعداد طولانی

همانطور که گفتیم در مورد اعداد طولانی نیز لازم نیست نگران باشید و وقتی عدد طولانی و بزرگی دیدید، گیج شوید و از آن بترسید!

فقط کافیست جایگاه عدد دهم و صدم بعد از ممیز را پیدا کنید و همان قواعد گرد کردن برای عدد های کوتاه را بر روی آنها اعمال کنید.
برای مثال:
گرده شده عدد 792323124.29 برابر 792323124.3 است.
گرد شده عدد 5.064213243215 برابر 5.1 است.
گرد شده عدد 9000.30001 برابر 9000.3 است.

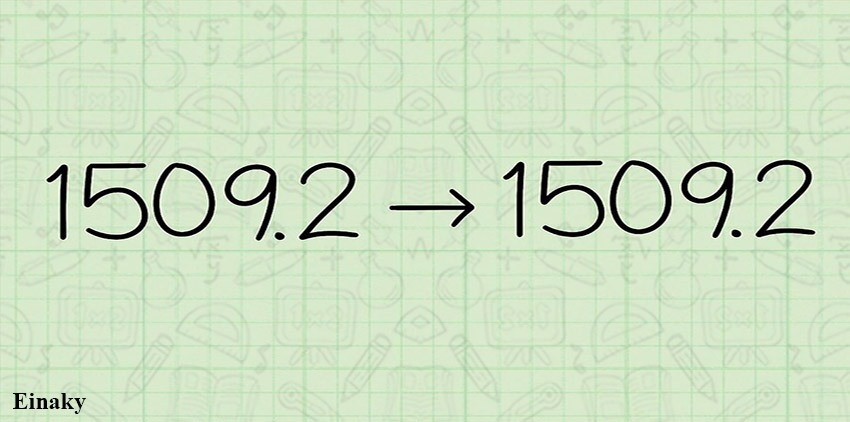
4- اگر عددتان فقط رقم دهم داشت چه کار باید کرد؟

اگر عدد شما فقط تا رقم دهم ادامه داشت به این معنی است که این عدد در حال حاضر گرد شده است و لازم نیست عملیات دیگری را روی آن انجام دهید.
برای مثال عدد 1052.9 گرد شده است و لازم نیست گرد شود.

جمع بندی
اگر بخواهید عدد اعشاری را گرد کنید تنها کافی است به عدد صدم، یعنی عدد دوم بعد از ممیز نگاه کنید و اگر بیشتر از 5 یا خود 5 بود یک رقم به عدد دهم آن اضافه کنید و اگر 4 یا کمتر از آن بود لازم نیست کاری انجام دهید.

در نهایت باید تمام عدد های بعد از ممیز به جز عدد دهم را پاک کنید. 

حتما بخوانید: پیشامدهای مستقل و ناسازگار

منبع: عینکی

حل معادله درجه دو به روش ضربدری

همانطور که می دانید برای حل معادله های درجه دو میتوان از روش تجزیه ، روش ریشه گیری، روش مربع کامل و روش دلتا استفاده کرد.

اما در این مقاله ” حل معادله درجه دو با استفاده از مجموع و حاصل ضرب ریشه ها یا روش ضربدری “، که روش جدیدی برای حل معادلات درجه دو می باشد را به شما آموزش خواهیم داد.

 حل معادله درجه دو با استفاده از مجموع و حاصل ضرب ریشه ها ، روشی بر مبنای آزمون و خطا است.  

این روش مشابه فاکتور گیری است با این تفاوت که تعداد حالت ها به نصف کاهش می یابد.
همچنین این روش برای معادله های درجه دومی که بتوان از آنها فاکتور گرفت مناسب می باشد.
دقت کنید که برای راحتی کار در معادله ax2 +bx+c = 0 ، علامت a را مثبت در نظر می گیریم.

 

مراحل حل معادله درجه دو به روش ضربدری

1- معادله درجه دوم دو ریشه دارد.

همانطور که میدانید در معادله درجه دو مجموع ریشه ها از رابطه (b/a-) و حاصل ضرب ریشه ها از رابطه (c/a) به دست می آید.

2- استفاده از قاعده علامت برای ریشه ها

برای اینکه تعداد انتخاب ها را کاهش دهیم میتوانید از قاعده زیر استفاده کنید:

اگر a و c مختلف العلامت باشند، هر دو ریشه نیز مختلف العلامت هستند.
به عنوان مثال در عبارت 6x2 – 11x – 35 = 0 دو ریشه مختلف العلامت هستند چون a=6 و c=-35 است.

اگر a و c هم علامت باشند، دو ریشه حقیقی هم علامت هستند و بعداً میتوانیم تشخیص دهیم که هر دو مثبت یا هر دو منفی هستند.

اگر a و b مختلف العلامت باشند هر دو ریشه مثبت هستند.

در عبارت 21x2 – 23x + 6 = 0 هر دو ریشه حقیقی مثبت هستند.

در واقع از این روش نمیتوانیم برای  معادلات درجه دو که ریشه حقیقی ندارند (مثل 21x2 – x + 6 = 0) استفاده کنیم.

اما میتوانیم بگوییم که اگر دو ریشه معادله حقیقی باشند، هر دو ریشه مثبت هستند.

اگر a و b هم علامت باشند هر دو ریشه منفی هستند.

برای مثال 15x2 + 22x + 8 = 0 دو ریشه دارد که هر دو منفی هستند.

مجدد ذکر میکنیم این روش برای ریشه های مرکب جواب نمیدهد.

3- فرض کنید که تساوی درجه دوم دو ریشه حقیقی گویا دارد، ریشه ها را به صورت عبارت کسری  با مخرج مثبت در عبارت بیان میکنیم.

اگر ریشه ها r/s و t/u باشند پس جمع مورب  ru+ts=-b میباشد. عبارت ru+ts جمع ضربدری (یا اریب) نامیده می شود.

نکته: در این فرمول a را مثبت در نظر می گیریم، اگر a منفی باشد ru+ts=b میشود.

اگر دو ریشه حقیقی-1/3 و 3/5 باشد جمع اریب آنها 4 = -5 + 9 =  (-1)*(5) + (3)*(3) میشود.
معادله درجه دوم  برای این عبارت 15x2 – 4x – 3 = 0 میباشد.

نکته: علامت b مخالف جمع اریب مورد انتظار میباشد.

4- از a و c فاکتور بگیرید.

تمام کسر هایی که در آنها صورت کسر برابر r.t =c و مخرج کسر برابر s.u =a را بنویسید.

با استفاده از قاعده علامت ها، علامت درست را برای کسر ها در نظر بگیرید.

در غیر این صورت اگر ریشه ها هم علامت نیستند نیازی به بررسی {1/3, -3/5} و {-1/3, 3/5} نیست.
اگر جمع اریب یا ضربدری یکی از دو جفت ریشه ها مقدار صحیح داشته باشد اما علامت آن اشتباه باشد پس جفت کسر دیگر جواب معادله است.

دقت کنید که فقط یکی از حالت ها جواب معادله درجه دو خواهد بود.

5- جمع اریب جفت کسرها را بررسی کنید.

اگر جمع اریب مساوی b- نباشد پس جواب است.

اگر جمع اریب مساوی b+ باشد، مخالف جواب است .

اگر جمع اریب b- یا b نباشد ریشه های معادله درجه دوم گنگ یا مرکب است و باید از روش های دیگر ریشه های آن را به دست آورد.

منبع: عینکی

چگونه شرایط را برای درس‌خواندن فراهم کنیم؟

سؤالی که همیشه برای دانش‌آموزان پیش می‌آید این است: تفاوت کسی که روز قبل از امتحان، ۱۰ ساعت مطالعه می‌کند با کسی که پنج روز و روزی دو ساعت می‌خواند، چیست؟ بسیار مهم است که دانش‌آموزان با کمک برنامه‌ریزی و استفاده‌ی مناسب از زمان، شرایط آرام و خوبی برای مطالعه فراهم کنند تا بتوانند بازدهی کارشان را تا حد امکان افزایش دهند.

بهتر است ابتدا مکان مناسبی برای درس‌خواندن انتخاب کنید. تنظیم نور و درجه‌حرارت و جایگاه نشستن شما بسیار مهم است. در ضمن، تمام وسایل موردنیازتان را در کنار خود بگذارید تا هنگام مطالعه تمرکز کافی داشته‌ باشید.

مدت‌زمانی را که برای مطالعه در روز در اختیار دارید، محاسبه کنید. هرشب قبل از خواب، فهرستی از کارهای روزانه‌ی خود را برای فردای آن روز آماده کنید و برای هرکدام از آن‌ها مدت‌زمانی را پیش‌بینی کنید. به این ترتیب، مدت‌زمانی که برای درس‌خواندن باقی‌ می‌ماند، مشخص خواهد شد.

درس‌هایتان را به‌ترتیب اهمیت و زمانی که می‌خواهید برای یادگیری آن‌ها صرف کنید، اولویت‌بندی کنید. تعادل به‌معنای تساوی نیست. تعادل وقتی رعایت می‌شود که درس و مبحثی را بیشتر بخوانید که نیاز بیشتری هم به توجه دارد. بهتر است هنگامی که بیشترین آمادگی ذهنی را دارید، دشوارترین درس را مطالعه کنید. استراحت بین وعده‌های مطالعاتی را جدی بگیرید و به کیفیت زمان استراحت خود فکر کنید.

شرایط دیگری که لازم است در برنامه‌ی درسی خود به آن توجه کنید، درنظرگرفتن زمان روزانه برای مرور درس‌های گذشته است. مرور به شما کمک می‌کند که با ذهن بازتری به سراغ حل تمرین و تست بروید.

منبع: قلم چی

اهمیت آزمون‌دادن در فرایند آموزش

آزمونْ راهی برای سنجش دانشِ دانش‌آموزان است. امتحانات تشریحی و تستی موجب می‌شود که دانش‌آموزان با تمرکز و توجه بیشتری درس بخوانند و یادگیریْ در سطح بالاتری اتفاق بیفتد. آزمونْ هدف است. دانش‌آموز برای کسب نمره‌ی بهتر در آزمون، خود را ملزم به حل سؤالات مختلف می‌کند و این امر موجب می‌شود تا با نگرشِ طراحانِ سؤال آشنا شود. به‌ این ترتیب، آزمون‌دادن عاملی برای یادگیریِ شیوه‌ی درست مطالعه‌ی هر درس می‌شود.

وقتی دانش‌آموز آزمون می‌دهد یا در منزل خودش را با تست‌ها و تمرین‌های متفاوت می‌آزماید، هر سؤال برای او مانند کلاس درس است. ابتدا با هر سؤال دانش خود را درباره‌ی مبحث موردنظر می‌سنجد و سپس در صورت نیاز آن را دوباره مطالعه می‌کند. مرحله‌ی دوم، مطالعه‌ی پاسخ سؤال است. این مرحله موجب می‌شود تا راه‌های دیگر و نکات جدیدتری از درس را یاد بگیرد و بتواند از این نکات جدید در حل سؤالات دیگر نیز استفاده کند.

در این میان، امتحانات جامع که دانش‌آموز در آن‌ها چند درس را در یک زمان مشخص امتحان می‌دهد نسبت به امتحانات تک‌درس برتری دارند؛ زیرا ذهن دانش‌آموز ورزیده‌تر می‌شود و آمادگی مغزش برای تفکیک و ترکیب اطلاعات افزایش می‌یابد. ذهن هم برای اینکه کارایی بهتری داشته باشد، به ورزش و تمرین منظم نیاز دارد. به همین دلیل است که همواره به دانش‌آموزان تأکید می‌شود پیش از شرکت در آزمون‌ها، در منزل، به‌قدر کافی و تحتِ شرایطِ آزمون، از خودشان امتحان بگیرند.

یکی دیگر از مزایای آزمون‌دادن، ایجاد انگیزه و شوق برای یادگیری بیشتر است. دانش‌آموزان صرف‌نظر از هر نتیجه‌ای که در امتحان به دست می‌آورند، برای تلاشِ بیشتر اشتیاق پیدا می‌کنند. اگر پیشرفت کرده باشند، به احساس توانمندی و اعتمادبه‌نفس می‌رسند و باز تلاش خود را بیشتر می‌کنند. اگر پیشرفت نکرده باشند، آزمون‌ها و امتحانات بعدی را فرصتی برای اثبات توانمندی‌ خود می‌دانند؛ بنابراین آزمون‌دادن لازمه‌ی تکمیل فرایند یادگیری است.

منبع: قلم چی

چطور ریاضی رو بخونیم؟

چطور خوندن ریاضی، سوالیه که هر دانش آموزی حداقل یک بار از خودش پرسیده. بعضی از دانش آموزان ریاضی رو دوست دارن، اما اگه بخوایم صادق باشیم، بیشتر مردم از ریاضی متنفرند.

برای خیلی از دانش آموزان، ریاضی اونقدر اهمیت نداره  که بخوان با علاقه دنبالش برن و خیلی ها فقط برای اینکه مجبورن، اون رو میخونن.

البته ریاضی توی خیلی از رشته های دانشگاهی هم تدریس میشه اما واقعیتی که وجود داره اینه که ما تقریباً به صورت روزانه داریم ازریاضیات استفاده می کنیم.

مشکلی که برای بسیاری از افراد وجو داره  اینه که نمیدونن چطور باید ریاضی رو خوند.

ریاضی، یکی از موضوعاتیه که به راحتی چندین ساعت از وقت ما رو میگیره،اما در نهایت ممکنه سر جلسه امتحان نتونیم به سوالات جواب بدیم و نمره خوبی نگیریم.

خوشبختانه، تکنیک هایی وجود داره که بدون توجه به اینکه در چه سطحی هستید با دونستن و به کار بردن اونها می تونید تو این زمینه موفق باشید.

نکاتی برای حل مسائل ریاضی

۱-تمرین و تمرین و تمرین

فقط گوش دادن و خوندن ریاضی کافی نیست. برای ریاضیات باید آستین ها رو بالا بزنید و مشکلاتی که سرراهتون هست رو حل کنید.

هرچه بیشتر مسائل ریاضی رو حل کنید،بهتره. هر سوال یک روش خاص برای حل کردن داره، بعضی مواقع میتونید یه سوال رو با چندین روش حل کنید.

تمرین میتونه به شما کمک کنه که سرجلسه امتحان با خیال آسوده تری به سوالات جواب بدید.

۲-بررسی اشتباهات

ممکنه در زمان حل مسئله،راه حلی که برای اون استفاده می کنید، اشتباه باشه، باید بررسی کنید که چرا به جواب اشتباه رسیدید و مشکل از کجا بوده.

دونستن این که کدوم قسمت از راه حل رو اشتباه رفتید، یه روش عالی برای قوی تر شدن در ریاضیه و اینکه دیگه اون اشتباه رو تکرار نمی کنید.

۳-درک روش های حل مسئله

سعی نکنید فرمول ها رو حفظ کنید.شاید حفظ کردن فرمول های ریاضی در کوتاه مدت، به شما در حل مسائل کمک کنه، اما در دراز مدت این طور نیست.

درک مفهوم و منطق ریاضی به شما کمک میکنه که بسیار بهتر مسائل مشابه رو تحلیل و درک کنید.

توجه داشته باشید ریاضی موضوعیه که با تکرار و تمرین میتوان در آن به تسلط رسید. قبل از اینکه بخواید فرمول های پیچیده رو درک کنید بهتره سراغ درک فرمول های ساده تر برید.

۴- پذیرش اشتباهات

خیلی وقتا، زمانی که دانش آموز شروع به حل مسئله ریاضی می کنه، یه راه حل رو اشتباه ادامه میده و میخواد با همون راه حل اشتباه به جواب برسه،اما به جای جواب به ناکجا آباد می رسه!

در زمان حل مسائل ریاضی به راه حل دقت کنید.وقتی میبینید راه حل اشتباهه دیگه ادامش ندید و وقتتون رو هدر ندید،به جای اون ببینید مشکل کجاست و روی آن تمرکز کنید.

به یاد داشته باشید ریاضی به صبر و زمان نیاز داره تا استاد

یه ایده خوب برای خوندن ریاضی اینه که با دوستاتون و به صورت گروهی سوالات رو حل کنید.

۵-انتخاب یک محیط خوب برای مطالعه

ریاضیات جزء موضوعاتی است که به تمرکز و دقت بالایی نیاز داره، سعی کنید محیطی که برای مطالعه ریاضی انتخاب می کنید، محیطی آرام و به دور از حواس پرتی باشه.

میتونید از یک موزیک ملایم هم در محیط مطالعه استفاده کنید.

۶- یک دیکشنری ریاضی درست کنید.

ریاضی دارای فرمول ها و اصطلاحات ریادی هست،تمام فرمول های ریاضی رو به همراه یه نمونه سوال از اون داخل یه دفتر به صورت خلاصه یادداشت کنید تا هر موقع که میخواید بتونید از اون استفاده کنید.

۷- ریاضیات را در زندگی واقعی ببینید.

سعی کنید ریاضیات رو به زندگی روزمرتون وارد کنید. مثلاً اینکه ریاضی چطور توی قرعه کشی یا بخت آزمایی مورد استفاده قرار می گیره.

درآخر فراموش نکنید که اعتماد به نفستون رو حفظ کنید و با امتحان رو به رو بشید و اطمینان داشته باشید که برای آزمون آمادگی کامل رو دارید.

حتما بخوانید: ۱۰ نکته برای موفقیت در درس ریاضی

منبع: عینکی