عدد و الگوهای عددی

1- الگوهای عددی

عددهای زوج: عددهایی که رقم یکان آنها،0،2،4،6،8 باشد را اعداد زوج می گویند.

• مثال: 7334-218-37590

 عددهای فرد: هر عدد طبیعی که زوج نباشد، فرد است.

مضرب یک عدد: از ضرب عددهای طبیعی در یک عدد، مضرب های آن عدد به دست می آید.

نکته: از ضرب عددهای طبیعی در 3، مضرب های 3 به دست می آید.

نکته: کوچکترین مضرب هر عدد خود عدد است.

• مثال: کوچکترین مضرب 7 عدد 7 و کوچکترین مضرب 18 خود عدد 18 است.

2- یاد آوری عدد نویسی

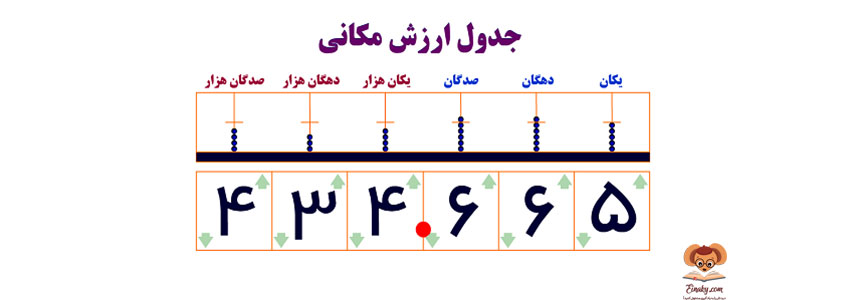
نکته: هر چه قدر به سمت راست جدول ارزش مکانی حرکت کنیم، ارزش مکانی رقم ها کمتر می شود.

نوشتن اعداد به حروف

ابتدا عدد را از سمت راست به چپ، سه رقم سه رقم جدا می کنیم و سپس با توجه به طبقه آنها را می خوانیم.

گسترده نویسی

برای گسترده نویسی کافی است هر رقم را در مرتبه آن ضرب کرده و بین رقم ها علامت + قرار دهیم.

• مثال: (1*5)+(10*9)+(100*3)=395

مقایسه ی عددهای صحیح

برای مقایسه ی دو عدد ابتدا به تعداد رقم هایش توجه می کنیم، هر عدد که تعداد رقم هایش بیشتر باشد بزرگتر است.

اگر تعداد رقم ها مساوی باشد، از اولین رقم سمت چپ مقایسه را شروع می کنیم و به سمت راست حرکت می کنیم.

3- بخش پذیری

بخش پذیری بر2: عددی بر 2 بخش پذیر است که رقم یکان آن 0،2،4،6،8 باشد.

بخش پذیری بر5: عددی بر 5 بخش پذیر است که رقم یکان آن صفر یا 5 باشد.

بخش پذیری بر3: عددی بر 3 بخش پذیر است که جمع رقم هایش بر 3 بخش پذیر باشد.

بخش پذیری بر 9: عددی بر 9 بخش پذیر است که جمع رقم هایش بر 9 بخش پذیر باشد.

بخش پذیری بر 6: عددی بر 6 بخش پذیر است که هم بر 2 و هم بر 3 بخش پذیر باشد.

نکته: هر عددی که بر 2 بخش پذیر باشد مضرب 2 است.

نکته: هر عددی که بر 5 بخش پذیر باشد مضرب 5 است.

نکته: اگر عددی هم بر 2 و هم بر 5 بخش پذیر باشد، آن عدد بر 10 بخش پذیر است.

نکته: رقم یکان عددی که هم بر 2 و هم بر 5 بخش پذیر است و یا رقم یکان عددی که بر 10 بخش پذیر است، صفر است.

نکته: باقی مانده تقسیم یک عدد بر 2، یا یک است یا صفر. اگر عدد زوج باشد باقی مانده صفر و اگر عدد فرد باشد باقی مانده یک است.

نکته: برای تعیین باقی مانده تقسیم یک عدد بر 5، فقط کافی است که باقی مانده تقسیم رقم یکان آن را بر 5 حساب کنیم.

نکته: باقی مانده تقسیم هر عدد بر 10 برابر است با رقم یکان عدد.

نکته: عددی که هم بر 3 و هم بر 5 بخش پذیر باشد بر 15 هم بخش پذیر است.

4- معرفی عددهای صحیح

در محور اعداد، نقطه مبدا را با عدد صفر نشان می دهیم.

عددهای سمت راست صفر را عددهای صحیح مثبت و عدد های سمت چپ صفر را عدد های صحیح منفی می نامیم.

نکته: روی محور هر چه در جهن مثبت پیش برویم عددها بزرگتر و هر چه به سمت منفی پیش برویم عددها کوچکتر می شوند.

نکته: بزرگترین عدد صحیح منفی، عدد 1- و کوچکترین عدد صحیح منفی وجود ندارد.

نکته: کوچکترین عدد صحیح مثبت، عدد 1+ و بزرگترین عدد صحیح مثبت مشخص نیست.

نکته: اگر عددی علامت نداشته باشد، علامت آن مثبت است.

نکته: قرینه یک عدد با خود آن عدد برابر است، فقط علامت آن تغییر می کند.

نکته: قرینه صفر خود صفر است.

نکته: عدد صفر علامت ندارد.

نکته: قرینه ی قرینه ی هر عدد با خود عدد برابر است.

حتما بخوانید: عدد های صحیح

منبع: عینکی

جمع و تفریق کسر ها

• توضیحات

جمع و تفریق کسر ها

مفهوم کسر

به جزء یا قسمتی از یک واحد کامل، کسری از آن واحد گفته می شود، بنابر این کسری از کل یعنی جز یا قسمتی از آن کل.

عدد مخلوط

اگر صورت کسر بزرگتر از واحدی، بر مخرجش بخش پذیر نباشد، آن کسر را می توان به صورت عدد مخلوط نوشت.

نکته: شکل درست یک عدد مخلوط، این است که حتماً کسر نوشته شده در عدد مخلوط کوچکتر از واحد آن باشد.

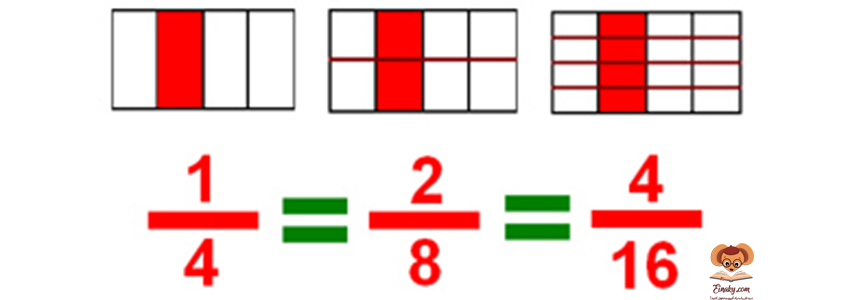
کسر های مساوی

اگر صورت و مخرج کسری را در عدد طبیعی بزرگتر از یک، ضرب و یا بر عدد طبیعی بزرگتر از یک تقسیم کنیم، کسر مساوی کسر اولیه به دست می آید.

نکته: برای هر کسر بی شمار کسر مساوی می توان نوشت.

کوچکترین مخرج مشترک دو یا چند کسر

اگر دو یا چند کسر داشته باشیم و بزرگترین مخرج این کسر ها بر بقیه ی مخرج ها بخش پذیر باشد، همان مخرج بزرگتر، کوچکترین مخرج مشترک کسر ها می شود.

نکته: روش بهتر برای یافتن کوچکترین مخرج مشترک دو کسر، این است که اگر بزرگترین مخرج بر دیگر مخرج ها بخش پذیر نبود،

آن را در عدد های 2،3،4 و… به ترتیب ضرب کنیم تا جایی که بر مخرج یا مخرج های دیگر بخش پذیر شود.

مقایسه ی کسر ها

اگر دو کسر دارای مخرج های مساوی باشند، کسری بزرگتر است که صورتش بزرگتر باشد.

نکته: اگر دو کسر دارای صورت های مساوی باشند، کسری بزرگتر است که مخرجش کوچکتر باشد.

نکته: برای مقایسه دو کسر که صورت آنها برابر نباشد و مخرج آن ها نیز برابر نباشد، از روش ضرب دری یا طرفین وسطین استفاده می کنیم.

مقایسه ی کسر ها توسط محور

در این روش دو محور رسم میکنیم که دقیقاً واحد های هم اندازه داشته باشند، و صفر های دو محور دقیقاً زیر هم قرار گیرند.

مقایسه ی دو کسر توسط شکل

 در این روش دو واحد برابر انتخاب می کنیم و سپس با توجه به مخرج کسر ها آن ها را به قسمت های مساوی تقسیم کرده و سپسکسر ها را روی شکل مشخص و مقایسه می کنیم.

1- جمع و تفریق کسر ها

در جمع و تفریق کسر ها، باید مخرج ها مساوی باشند و اگر مخرج ها مساوی نبودند با استفاده از کوچکترین مخرج مشترک آنها، مخرج هایشان را مساوی می کنیم.

جمع اعداد مخلوط

برای جمع اعداد مخلوط بهتر است اعداد صحیح را با هم و کسر ها را نیز با هم جمع کنیم.

تفریق اعداد مخلوط

همانند جمع اعداد مخلوط بهتر است، عدد های صحیح را از هم و کسر ها را نیز از هم کم کنیم.

2- ضرب کسر ها

در ضرب دو یا چند کسر باید صورت ها را در هم و مخرج ها را نیز در هم ضرب کنیم.

نکته: در ضرب کسر ها، اگر بتوانیم صورت ها را با مخرج کسر ها ساده کنیم، بهتر است این کار را انجام دهیم و سپس حاصل ضرب را حساب کنیم.

ضرب عددهای مخلوط

برای ضرب عددهای مخلوط، ابتدا اعداد مخلوط را به کسر تبدیل کرده و سپس کسر ها را در هم ضرب می کنیم و حاصل را به دست می آوریم.

نکته: هر گاه حاصل ضرب دو عدد مساوی یک باید فآن دو عدد معکوس یکدیگرند.

نکته: همه عددها به جز صفر معکوس دارند.

نکته: اگر بخواهیم معکوس یک عدد مخلوط را مشخص کنیم، ابتدا باید آن را به شکل کسر بنویسیم و سپس کسر را معکوس کنیم.

نکته: نصف یک عدد یعنی آن عدد ضرب در  یک دوم

نکته: ثلث یک عدد یعنی آن عدد ضرب در یک سوم

نکته: ربع یک عدد یعنی آن عدد ضرب در یک چهارم

نکته: خمس یک عدد یعنی آن عدد ضرب در یک پنجم

3- تقسیم کسر ها

برای محاسبه ی تقسیم کسر، کسر اول را نوشته تقسیم را به ضرب تبدیل کرده و کسر دوم را معکوس می کنیم، سپس مانند ضرب کسر هاحاصل را به دست می آوریم.

نکته: اگر در تقسیم کسر ها، صورت کسر سمت چپ بر صورت کسر سمت راست و مخرج کسر سمت چپ  بر مخرج کسر سمت راستبخش پذیر باشد،

می توانیم آن ها را بر هم تقسیم کنیم و جواب را به دست آوریم.

تقسیم کسر ها با شکل و به کمک محور

هر دو این روش ها در فیلم آموزش ریاضی ششم با مثال توضیح داده شدن.

4- محاسبات با کسر ها

محاسبه کسر ها به روش مخرج مشترک گرفتن

محاسبه کسر با کمک محور

محاسبه کسر با رسم شکل

حتما بخوانید: عدد و الگوهای عددی

منبع: عینکی

بخش پذیری بر 15:  عددی بر 15 بخش پذیر است که هم بر 3 و هم بر 5 بخش پذیر باشد.

منبع:عینکی 

12 راهبرد برای انگیزه‌بخشی به فرزندان در یادگیری (11)

اغلبِ دانش‌آموزانِ خوب، یادگیرندگانِ خوبی به دنیا نمی‌آیند. بله. ویژگی‌های شخصیتی فرد نقش مهمی در آمادگی او برای یادگیری و موقعیت کلی در تحصیل و آموزش دارد؛ اما اغلب بچه‌هایی که دانش‌آموزان خوبی هستند، در بعضی مسائل، یادگیرندگان خوبی هم هستند. مهم‌تر از همه این‌که دانش‌آموزی که استعدادهای بنیادی دارد و به‌درستی به او انگیزه داده می‌شود، می‌تواند دانش‌آموز خوبی باشد.

یکی از اشتباهاتی که دبیران و والدین ممکن است در حق دانش‌آموزان و فرزندانِ روبه‌پیشرفتِ خود مرتکب ‌شوند این است که آموزشِ آن‌ها را به کلاس درس محدود کنند. هرچند کلاسِ درس منبع اصلی آموزش است، اگر واقعاً می‌خواهید توانایی و تمایل فرزند خود را به یادگیری افزایش دهید، رشد ذهنی، اجتماعی و تحصیلی باید خارج از محیط کلاس گسترش یابد.

در ادامه، نکات و راهبردهای اثبات‌شده‌ای آمده است که به فرزندان شما انگیزه‌ی یادگیری می‌دهد. آن‌ها را به‌درستی به کار ببندید؛ دراین‌صورت خواهید دید که فرزند یا دانش‌آموز شما لذت یادگیری را کشف خواهد کرد.

11. بر نقاط قوت تمرکز کنید

‌زمانی که فرزندتان دچار کشمکش‌های تحصیلی است، تمرکز بر نقاط قوت بسیار دشوار است. با وجود این،‌ تمرکز بر نقاط قوت برای سلامتِ ‌عاطفی و رشد و پیشرفت تحصیلی او بسیار اساسی است. تمرکز بر نقاط قوت فرزندان یکی دیگر از روش‌های تقویتِ مثبت است که برای ادامه‌ی یادگیری‌ به او انگیزه می‌دهد.

برعکس، تمرکز بر نقاط ضعف برای فرزندتان چیزی جز دلسردی و ‌اضطراب و بی‌میلی به یادگیری به همراه ندارد. آیا فرزندتان در امتحان ریاضی مردود شده است؟ پس، علاوه بر کمک کردن بیش‌تر به او در درس ریاضی،‌ مطمئن شوید که او را برای عملکرد خوبش در درس علوم تشویق کرده‌اید.

منبع: قلم چی

12 راهبرد برای انگیزه‌بخشی به فرزندان در یادگیری (12)

اغلبِ دانش‌آموزانِ خوب، یادگیرندگانِ خوبی به دنیا نمی‌آیند. بله. ویژگی‌های شخصیتی فرد نقش مهمی در آمادگی او برای یادگیری و موقعیت کلی در تحصیل و آموزش دارد؛ اما اغلب بچه‌هایی که دانش‌آموزان خوبی هستند، در بعضی مسائل، یادگیرندگان خوبی هم هستند. مهم‌تر از همه این‌که دانش‌آموزی که استعدادهای بنیادی دارد و به‌درستی به او انگیزه داده می‌شود، می‌تواند دانش‌آموز خوبی باشد.

یکی از اشتباهاتی که دبیران و والدین ممکن است در حق دانش‌آموزان و فرزندانِ روبه‌پیشرفتِ خود مرتکب ‌شوند این است که آموزشِ آن‌ها را به کلاس درس محدود کنند. هرچند کلاسِ درس منبع اصلی آموزش است، اگر واقعاً می‌خواهید توانایی و تمایل فرزند خود را به یادگیری افزایش دهید، رشد ذهنی، اجتماعی و تحصیلی باید خارج از محیط کلاس گسترش یابد.

در ادامه، نکات و راهبردهای اثبات‌شده‌ای آمده است که به فرزندان شما انگیزه‌ی یادگیری می‌دهد. آن‌ها را به‌درستی به کار ببندید؛ دراین‌صورت خواهید دید که فرزند یا دانش‌آموز شما لذت یادگیری را کشف خواهد کرد.

12. هر روز را به روزی برای آموختن تبدیل کنید

اگر هر روز را به روزی برای یادگیری تبدیل کنید، ممکن است روزهای‌تان کمی شبیه به هم شوند؛ اما اگر از مسیر درستی بروید، این‌طور نخواهد شد. هر وقت امکان‌پذیر بود، از فرزندتان بخواهید جهان پیرامونش را کشف کند. از او سؤالاتی بپرسید و با او ارتباط برقرار کنید. در دسته‌بندی‌کردن و مرتب‌کردن و تفکر نقاد درباره‌ی هر آن‌چه می‌بیند و تجربه می‌کند، به او کمک کنید. تبدیلِ هر روز به روزی برای یادگیری، انگیزه‌ی درونیِ‌ او را برای یادگیری در کلاس و خانه و هر جای دیگری افزایش می‌دهد.

منبع: قلم چی